Pasos Para Resolver Un Problema Matemático – Orientacionandujar – ¡Bienvenidos a Pasos para resolver un problema matemático! Esta guía está diseñada para brindarles a los estudiantes las herramientas y estrategias necesarias para abordar cualquier problema matemático con confianza. Desde la comprensión del problema hasta la verificación de la solución, cubriremos cada paso en detalle para ayudarlos a dominar el arte de la resolución de problemas.
Al seguir los pasos descritos en esta guía, podrán mejorar significativamente sus habilidades para resolver problemas, desarrollar su pensamiento lógico y alcanzar el éxito en sus estudios de matemáticas.
Desarrollo de la Solución: Pasos Para Resolver Un Problema Matemático – Orientacionandujar
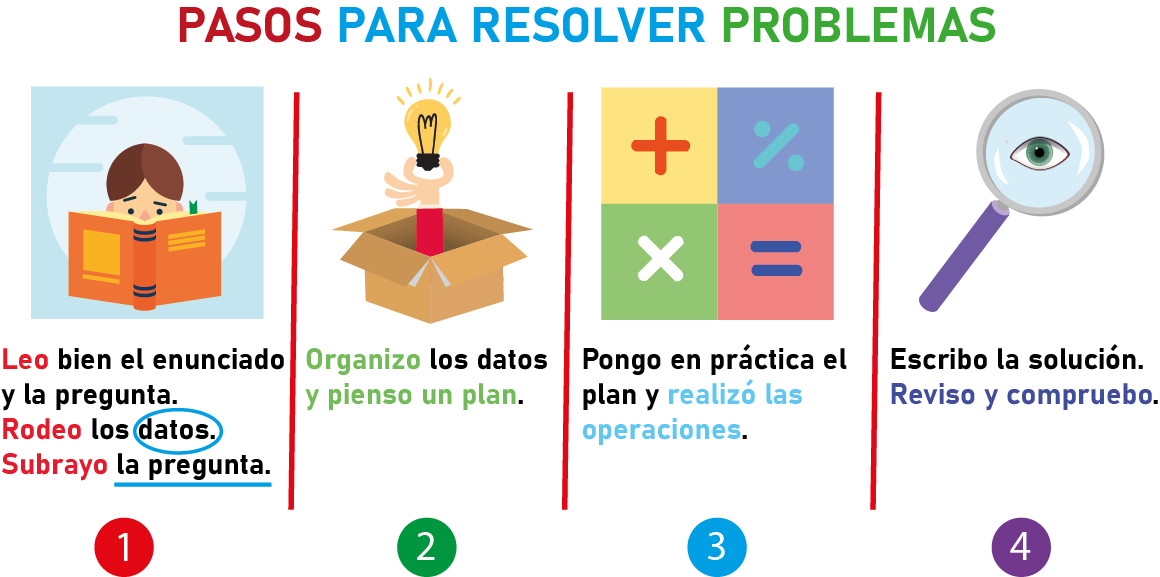
En esta etapa, aplicamos técnicas y herramientas para encontrar la solución al problema matemático. Es crucial ser sistemático y organizado para garantizar la precisión y la eficiencia.
Las tablas y los diagramas son herramientas valiosas para organizar datos y visualizar información compleja. Las fórmulas y ecuaciones proporcionan un marco matemático para modelar y resolver problemas.
Crear Tablas

Las tablas son útiles para organizar datos numéricos y realizar cálculos. Permiten agrupar y comparar información de manera estructurada.
- Define las columnas y filas de la tabla según los datos que necesitas organizar.
- Ingresa los datos en las celdas correspondientes.
- Utiliza fórmulas para realizar cálculos y resumir los datos.
Utilizar Diagramas y Gráficos, Pasos Para Resolver Un Problema Matemático – Orientacionandujar
Los diagramas y gráficos ayudan a visualizar información y relaciones. Facilitan la comprensión de patrones y tendencias.
- Elige el tipo de diagrama o gráfico más adecuado para los datos que tienes.
- Etiqueta los ejes y proporciona una leyenda clara.
- Analiza el diagrama o gráfico para identificar patrones y extraer conclusiones.
Explicar el Uso de Fórmulas y Ecuaciones

Las fórmulas y ecuaciones son herramientas matemáticas que permiten modelar y resolver problemas. Proporcionan una estructura para relacionar variables y calcular valores desconocidos.
- Identifica las variables y constantes involucradas en el problema.
- Aplica la fórmula o ecuación adecuada para relacionar las variables.
- Sustituye los valores conocidos y resuelve para las variables desconocidas.
“Las fórmulas y ecuaciones proporcionan un lenguaje universal para representar y resolver problemas matemáticos.”
Comprobación y Reflexión
Una vez que hemos obtenido una solución a un problema matemático, es esencial comprobar su exactitud y reflexionar sobre el proceso de resolución para identificar posibles errores y áreas de mejora.
La comprobación implica verificar que la solución obtenida satisface las condiciones del problema original y que no hay contradicciones lógicas.
Técnicas de Comprobación
- Sustitución: Sustituir la solución en la ecuación o expresión original y verificar si se obtiene el resultado esperado.
- Estimación: Realizar una estimación aproximada de la solución y compararla con el resultado obtenido.
- Comprobación inversa: Resolver el problema desde el final hasta el principio, utilizando la solución obtenida como punto de partida.
Errores Comunes
- Errores de cálculo: Errores en operaciones aritméticas básicas, como suma, resta, multiplicación o división.
- Errores de transcripción: Errores al copiar o escribir números o símbolos.
- Errores conceptuales: Errores en la comprensión de los conceptos matemáticos subyacentes al problema.
Reflexión sobre el Proceso de Resolución
La reflexión sobre el proceso de resolución implica analizar los pasos tomados, identificar posibles alternativas y buscar formas de mejorar la eficiencia y la claridad de la solución.
- ¿Se podría haber resuelto el problema de una manera más sencilla o eficiente?
- ¿Hay alguna técnica o concepto que podría haber facilitado la resolución?
- ¿Se pueden generalizar los métodos utilizados a otros problemas similares?
Resolver problemas matemáticos no tiene por qué ser una tarea abrumadora. Siguiendo los pasos descritos en esta guía, pueden abordar cualquier problema con confianza, desarrollar sus habilidades para resolver problemas y lograr el éxito en sus estudios de matemáticas. Recuerden, la práctica es clave, así que practiquen regularmente y no duden en buscar ayuda cuando la necesiten.
